La siguiente graduación en dificultad en el cálculo de las suma estás pormenorizada para que cualquier alumno pueda seguir una progresión en su aprendizaje que le garantice llegar hasta un nivel del cálculo personal. Por tanto está pensada para facilitar dicho tramite al alumnado que presente dificultades, ya que la mayoría del alumnado no será necesario seguir tan concienzudamente esta graduación, ya que la realizarán en bloques y no en pasos como se refleja en ésta tabla.

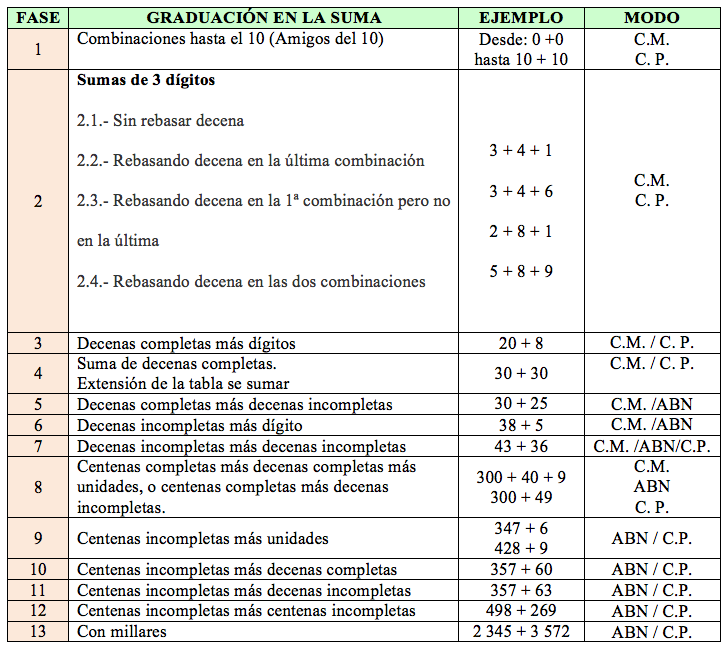
La última columna hace referencia al tipo de cálculo que realizará el alumnado en esa fase y que va desde el cálculo manipulativo «C.M». en el que necesitará apoyo de objetos para contar (palillos, cuentas,…), continuará con el cálculo en la rejilla «ABN», es decir el cálculo escrito y terminará en el cálculo pensado «C.P.» en el cual mentalmente realizará la operación. Se debe tener en cuenta que éste cálculo es evolutivo y se refleja la evolución dentro de las distintas fases

En esta secuenciación se establece una descripción de los pasos, una ejemplificación y dos modos de resolución, el cálculo mental y el algoritmo ABN, aunque la secuenciación es igualmente válida para el algoritmo tradicional.

Al final del artículo hay algunas indicaciones sobre las sumas que complementan la tabla aquí presentada.

DESCARGAR EL DOCUMENTO EN PDF

A partir del paso 12, el tipo de sumas que pueden surgir no añaden nada nuevo en el aprendizaje de la suma, pero además no tienen sentido realizarlas con ningún tipo de algoritmo que no sea el de la calculadora, ya que en la vida real no están presentes desde hace muchísimos años más allá del cálculo mediante el uso de estas ayudas digitales. Hemos incluido un último paso para las sumas con millares que puede verse cómo realizarlas en el vídeo tutorial «Operaciones mayores a las decenas de millar«.

Cuando hablamos de realizar las operaciones mediante el cálculo mental, es necesario realizarlo mediante el aprendizaje de la tabla de sumar, la cual puede ser complementada con las primeras series de cálculo mental del método Quinzet, las cuales facilitarán su aprendizaje y afianzamiento.

Bibliografía: «Competencias básicas en matemáticas. Una nueva práctica». Autor: Jaime Martínez Montero. Editorial Wolters Kluwer España.