En esta ocasión presento una actividad que he desarrollado con mi alumnado de 6º de Primaria con la cual les he abierto las puertas del aprendizaje de los conceptos de mínimo común múltiplo y máximo común divisor. Para ello les he pedido que lleven una baraja de cartas española. Previamente hemos trabajado los conceptos de números primos así como los criterios de divisibilidad, condición no imprescindible pero que agilizará mucho el proceso su conocimiento y dominio.

Los pasos a seguir se exponen a continuación y las actividades aunque ellos las han realizado individualmente, también se pueden realizar en parejas o en pequeños grupos.

APRENDEMOS A FACTORIZAR CON LAS CARTAS

Empezamos extrayendo de la baraja todos los números primos de todos los palos, es decir las cuatro cartas correspondientes al 2,3,5,7, y 11.

El primer juego consiste en formar números a partir del producto de las cartas de que disponemos. La graduación de dificultad que facilitará la adquisición progresiva del procedimiento sería:

1.- Números con el producto de dos cartas (factores primos).
2.- Números con el producto de tres cartas.
3.- Números con el producto de tres cartas en las que se repita una de ellas.
4.- Generalización a cualquier cantidad de cartas y repeticiones.

A continuación hemos realizado el proceso inverso. Ya sabemos que cartas son los factores que nos determinan sus productos, ahora le proporcionaremos el número y les pediremos que busquen las cartas cuyos productos nos den dicho número.

1.- Números cuya factorización sean dos números primos distintos. Ejemplo: 6, 10, 14, 15, 21, …
2.- Números cuya factorización sean dos números primos iguales. Ejemplo: 4, 9, 25, 49, 121…
3.- Números cuya factorización sean tres números primos distinto. Ejemplo : 30 (2,3 y 5), 42 (2,3 y 7), 66 (2,3 y 11), 70 (2,5 y 7), 110 (2,5 y 11),…
4.-  Números cuya factorización sean dos números primos distinto uno de los cuales pueda repetirse. Ejemplo: 12 (2,2,3), 18 (2,3,3), 36 (2, 2,3,3),…
5.- Generalización.

OBTENEMOS EL MÍNIMO COMÚN MÚLTIPLO CON LAS CARTAS

Con las actividades anteriores el alumnado ha practicado la factorización de números. A continuación hacemos lo mismo con dos números a la vez para practicar la obtención del mínimo común múltiplo.

Cuando tengamos la factorización de los dos números en dos grupos de cartas (factores primos) les indicaremos que busquemos aquella carta o cartas que estén repetidas en ambos grupos,  y descartaremos de ellas la que tenga menor cantidad de cartas, con lo cual el producto del resto de las cartas nos indicará el m.c.m.

Un ejemplo: Calcular el m.c.m. de 6 y 30. Buscamos las cartas de sus factores primos

A continuación descartamos las cartas que coinciden en ambos grupos y las demás las multiplicamos, obteniendo con ello el m.c.m.

La pregunta ahora es: ¿por qué hemos descartado esa carta y no otras?. Para la respuesta simplemente tomamos alguna de las cartas descartadas y la incluimos en la multiplicación anterior, lo cual nos dará un nuevo múltiplo, pero comprobaremos que no es el menor buscado. De esta forma ven el sentido del descarte de los números repetidos.

Veamos otros ejemplos para obtener el m.c.m.

Calcular el m.c.m. de 18 y 30. En primer lugar factorizamos ambos números.

Ahora retiramos la menor cantidad del número que se repite en ambos grupos.

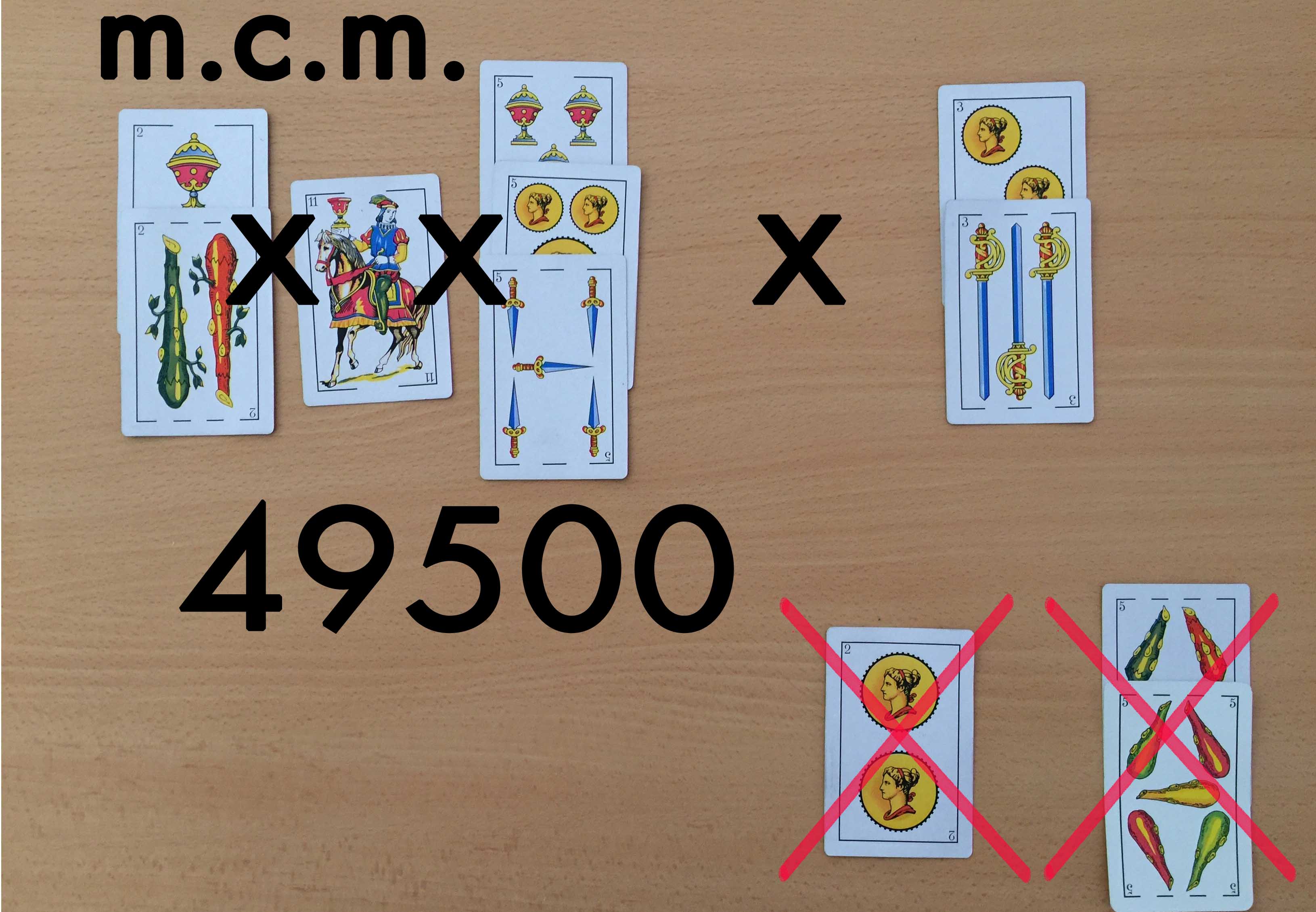
Y otro ejemplo para calcular el m.c.m. con cantidades mayores: 5500 y 450, siguiendo el mismo procedimiento anterior.

Tras el descarte calculamos el m.c.m.

OBTENEMOS EL MÁXIMO COMÚN DIVISOR CON LAS CARTAS

El procedimiento se adivinará que es exactamente igual, pero con la única excepción que ahora sólo nos quedaremos con la/s carta/s que se encuentren en menor cantidad en ambos grupos. Veamos cómo proceder con los anteriores ejemplos.

Un ejemplo: Calcular el m.c.d. de 6 y 30. Buscamos las cartas de sus factores primos.

El m.c.d de 6 y 30 es:

Calcular el m.c.d. de 18 y 30. Buscamos las cartas de sus factores primos.

El m.c.d de 18 y 30 es:

Calcular el m.c.m. de 5500 y 450. Buscamos las cartas de sus factores primos.

El m.c.d de 5500 y 450 es:

Una vez el alumno sabe cómo operar, el uso de los números primos para factorizar y el significado del mínimo común múltiplo y del máximo común divisor, sólo queda mostrarles cómo realizarlo sin las cartas y cómo los factores son los mismos que con ellas.

Este contenido se publicó por primera vez en actiludis.com el 28/10/2016