Al llegar a la tabla del seis comienzan los problemas cuando nos basamos en métodos exclusivamente memorísticos en los cuales priman los codos frente a otras alternativas. Es a partir de aquí cuanto el alumnado que no hemos conseguido «enganchar» se nos descuelga del todo, llegando a ser un auténtico calvario, además de convertirse en sí mismas en un fin y no en un instrumento para aplicar en el cálculo.

Si hemos seguido el consejo repetido varias veces en esta guía y hemos aplicado la propiedad conmutativa desde el principio, no sólo cuando preguntamos por las distintas tablas hasta el cinco, sino incluyendo en las operaciones productos del tipo 34 x 8, 245 x 6,… sin que hayamos llegado aún a estas tablas, el alumnado tiene el camino casi terminado, sólo queda rematar con todos los productos en los que ambos factores superen el seis.

A partir de aquí usaremos un procedimiento manual para aprender las tablas del 6, 7 8 y 9. Para ello trabajaremos el método de los dedos válido y eficaz para todas las combinaciones posibles de los números 6, 7, 8 y 9, pero no para cualquier otro número menor (esas combinaciones ya las sabe. Por ejemplo 8 x 4 y lo hemos trabajado con 4 x 8).

Para representar los números mayores de seis levantamos los dedos que corresponden a cada número (ver imagen), por ejemplo para el  6 le corresponde una mano con todos los dedos completos y otra mano con un solo dedo subido, para el 7 lo mismo pero con dos dedos subidos en una de las manos y así con el 8 y el 9. De esta representación sólo nos quedaremos con la mano que no tiene los cinco dedos extendidos.

Esta representación la repetimos en la otra mano con el segundo factor, por lo que -por ejemplo- el producto de 8 x 7 quedaría representado así:

La cantidad de dedos extendidos representan decenas , en nuestro ejemplo: 3 + 2  = 5 (decenas),  es decir 50.

A continuación nos fijamos en los dedos contraídos que representan productos menores de cinco, por tanto sencillos y conocidos ya por el alumnado. En nuestro ejemplo 2 x 3 = 6

Por tanto el resultado final de la representación mediante los dedos queda como 8 x 7 = 50 + 6 = 56.

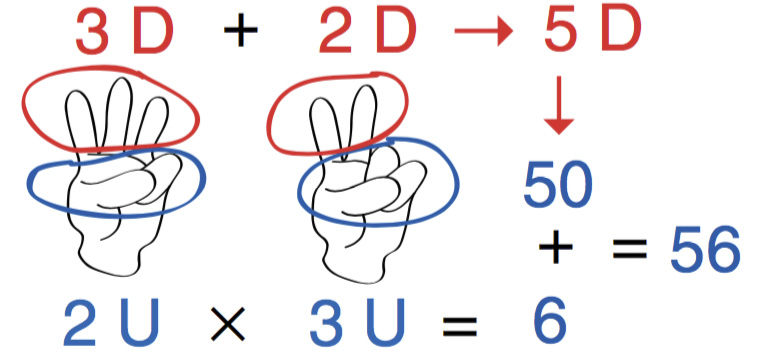
Hay que hacer notar que este procedimiento puede resultar engorroso al profesorado, simplemente porque cuando piensa en 8 x 7, en su mente se «ilumina» el 56, por que conoce el resultado. Debemos ponernos en la piel del alumnado y sobre todo del alumnado con problemas de aprendizaje de estas tablas para darnos cuenta que cuando a ellos le preguntamos por 8 x 7 en su cabeza no se «ilumina» absolutamente nada, por lo que este procedimiento es una balón de oxigeno y un medio para poder resolver operaciones como el producto y la división que hasta el momento de aprenderse las tablas le  estaban vetadas. Sólo la práctica hará que finalmente aprenda las tablas y en todo caso siempre tendrá un recurso fácil que llevará en sus manos si necesita algún producto de este tipo.

Tanto el procedimiento como la ejercitación del mismo con numerosos ejercicios los podemos encontrar en el libro de texto de 2º de Primaria de la editorial Anaya.

Para los más curiosos dejo a continuación un enlace que publicó Juan Durán en el Facebook ABN del blog «Matemáticas cercanas» de Amadeo Artacho Rocha titulado «¿Por qué “funciona” la multiplicación con los dedos?»

ENLACES CON ACTIVIDADES PARA TRABAJAR LAS TABLAS DEL 6, 7, 8 Y 9

Las tablas del 6, 7, 8 y 9 con los dedos

Mural producto con los dedos

GUÍA PARA EL APRENDIZAJE DE LAS TABLAS DE MULTIPLICAR

Esta guía consta de los siguientes artículos

1.- Planteamientos previos.
2.- Construcción y extensión de la tabla del 2.
3.- Sentamos las bases del producto con la tabla del 2.
3.- Las tablas del 3, 4 y 5.
4.- Las tablas altas y el producto con los dedos.
5.- El producto de las tablas del 11 y 12 (Próximo),

Imagen fuente: Libro de texto «Matemáticas ABN 2º de Primaria» Editorial Anaya

Bibliografía: «Competencias básicas en matemáticas. Una nueva práctica« Autor: Jaime Martínez Montero 2008) Madrid: Wolters Kluwer.