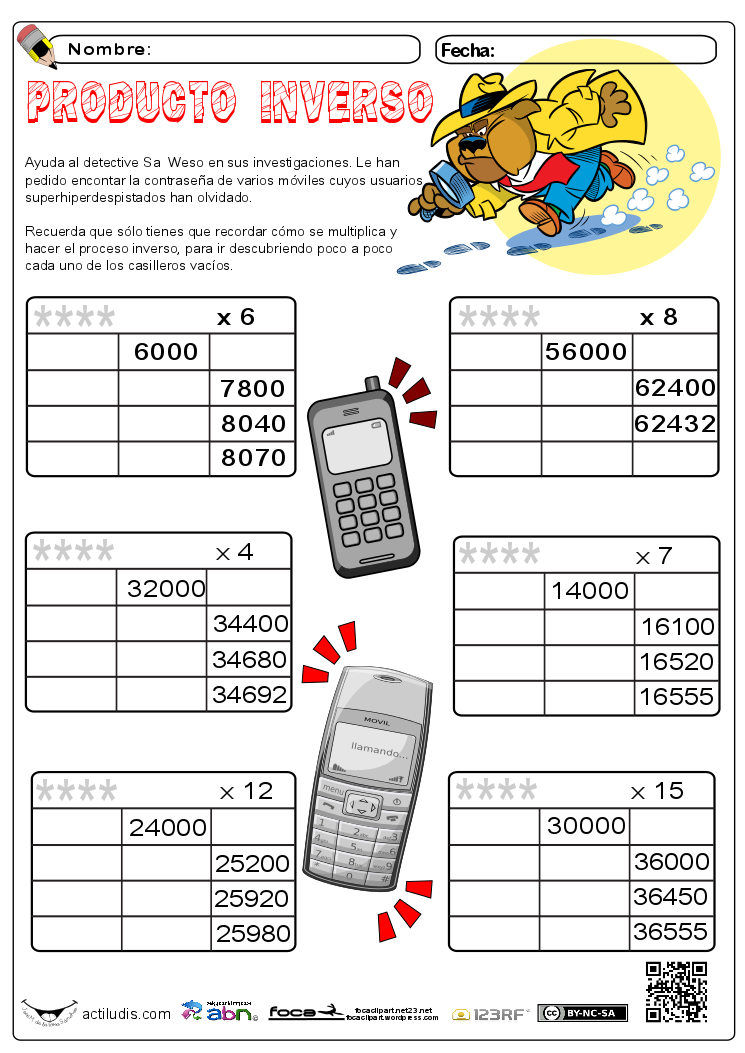
Producto inverso
El producto inverso es un cálculo que se desarrolla a partir de cuarto de Primaria con alumnos que trabajan el método ABN. Se trata de partir de sumas de productos parciales que conocemos para descubrir el primer factor de la multiplicación que desconocemos.
Podríamos simplemente dividir el producto final entre el factor que conocemos, pero esto sería una operación rápida y eficaz que no permite desarrollar otras herramientas que el producto inverso sí usa, así como provocar el razonamiento del alumnado. Es por tanto un cálculo que interesa trabajar y con el que el alumnado disfruta mucho, ya que lo montamos en formato detective.
Básicamente con esta forma de calcular desarrollamos la división como producto inverso y la resta dentro de la suma. Para aquellos que desconocen en que consiste a continuación de la ficha de trabajo desarrollo un ejemplo en el que queda suficientemente explicado.
DESCARGAR: «PRODUCTO INVERSO«
DESCARGAR: «SOLUCIÓN«
REALIZAR LA ACTIVIDAD ONLINE
He incluido el acceso al servicio de «Live Worksheets» para realizar la ficha online sin necesidad de imprimir, gracias al trabajo realizado por exceluisabn de Luis Millán Valdovinos
PROCEDIMIENTO DE CÁLCULO DEL PRODUCTO INVERSO
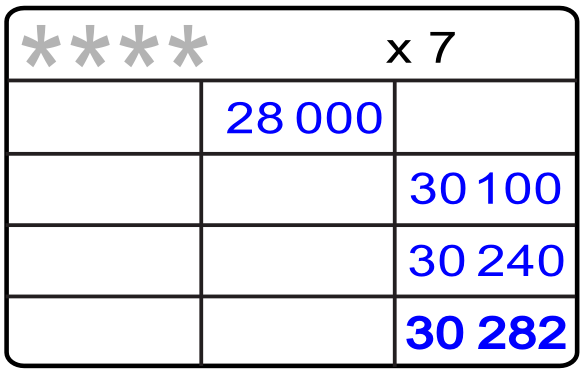
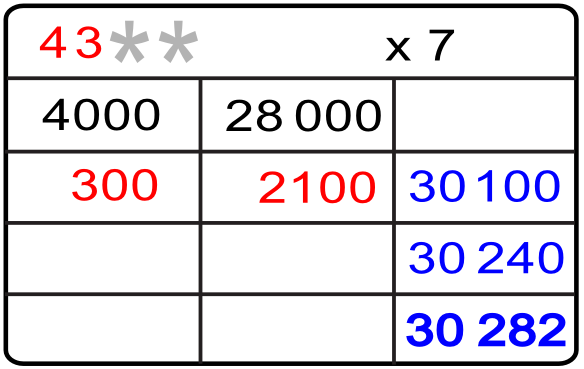
En el siguiente ejemplo vamos a ir reconstruyendo el producto con los datos que se nos proporcionan. La última columna refleja las sucesivas sumas de los productos parciales que nos han permitido llegar al producto final, siendo la cifra que aparece en la celda intermedia el primer producto parcial.
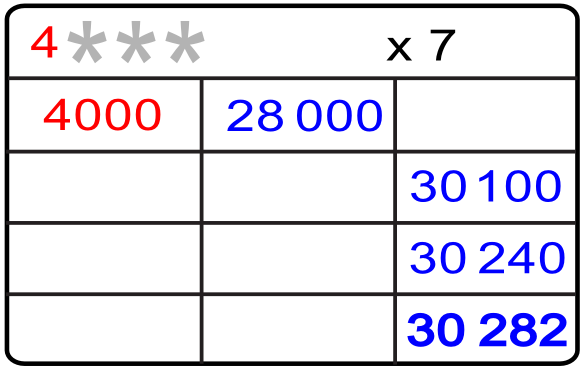
1.- Nos preguntamos cuál es el número que al multiplicarlo por 7 nos da el primer producto parcial de 28 000, o lo que es lo mismo 28 000 dividido entre 7.
2.- La respuesta es 4000 con lo que ya conocemos la primera cifra «4» del factor multiplicativo.
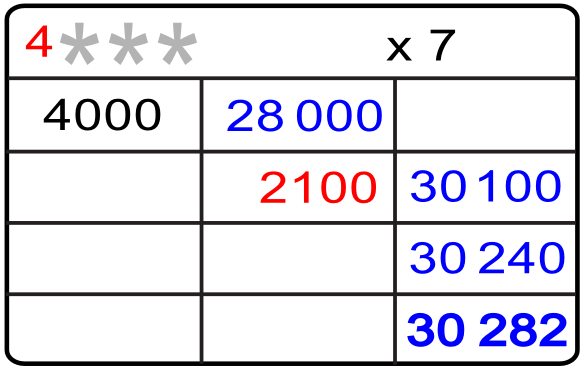
3.- Ahora nos preguntamos cuál es el segundo producto parcial que desconocemos, pero conocemos la primera suma de los dos primeros productos parciales, es decir 28 000 + ¿? = 30 100, por lo que de esta suma obtenemos mediante una recta el número que buscamos 30100 – 28000 = 2100
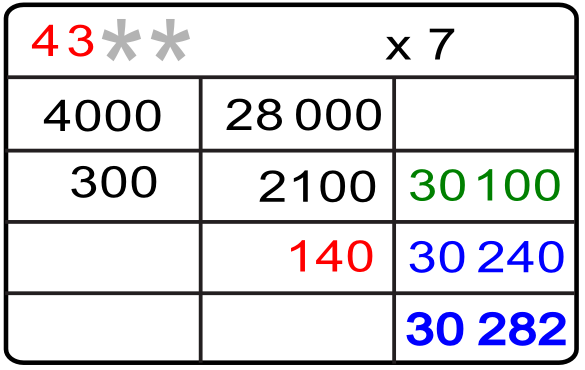
4.- Conocido el segundo producto parcial repetimos la pregunta inicial, ¿por cuánto multiplicamos 7 para obtener 2100? o simplemente dividimos 2100 entre 7 y las respuesta es 300. Ya conocemos la segunda cifra «3» del primer factor multiplicativo.
5.- Ahora vamos por el tercer producto parcial, el cual es la diferencia del 30 240 respecto a los dos productos parciales anteriores 28 000 + 2100 (30 100). Dicho producto es 30 240 – 30 100 = 140.
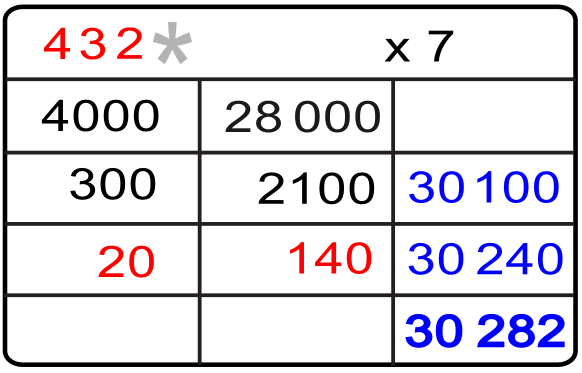
6.- Conocido el tercer producto parcial repetimos la pregunta inicial, ¿por cuánto multiplicamos 7 para obtener 140? o simplemente dividimos 140 entre 7 y las respuesta es 20. Ya conocemos la tercera cifra «2» del primer factor multiplicativo.
7.- Vamos a por el último producto parcial, el cual es la diferencia del 30 282 respecto a los tres productos parciales anteriores 28 000 + 2100 + 140 (30 240). Dicho producto es 30 282 – 30 240 = 42.
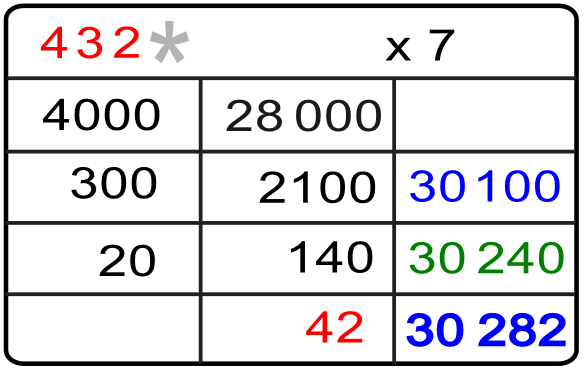
8.- Conocido el último producto parcial repetimos la pregunta inicial, ¿por cuánto multiplicamos 7 para obtener 42? o simplemente dividimos 42 entre 7 y las respuesta es 6. Ya conocemos la tercera cifra «6» y completamos el primer factor multiplicativo: 4326
Como podemos observar durante todo el proceso, aquí aplicamos conocimientos de operaciones inversas que el alumnado sabe y que aquí practica además de añadir un componente de razonamiento que el alumnado lo vive como un juego de detectives matemáticos.







Deja una respuesta