Tratamos en éste artículo el tema de las regletas Cuisenaire y su uso dentro de la metodología de cálculo ABN debido a que en numerosas ocasiones, tanto en los cursos de formación como a través de las redes sociales, se nos ha planteado su compatibilidad con el ABN.

De entrada, y más adelante lo desarrollamos, nuestra posición respecto al planteamiento de usarlas para trabajar numeración y cálculo ABN es desfavorable en lo que se refiere al material en sí, pero no a las innumerables actividades que se pueden realizar.

Cuando Georges Cuisenaire creó las regletas en 1952, fue con el fin de hacer algo más transparente el cálculo tradicional. Para eso nacen y para eso cumplen un papel importante dentro del algoritmo tradicional, y facilitando su comprensión el profesor Fernández Bravo hace un gran trabajo. Sin embargo el cambio metodológico del ABN, frente al cálculo tradicional, implica que la importancia que tal material puede tener en los nuevos planteamientos sea distinta, existiendo materiales muchos más eficaces y clarificadores para el alumnado, como son por ejemplo los bloques encajables de construcción y  los bloques multilink o policubos.

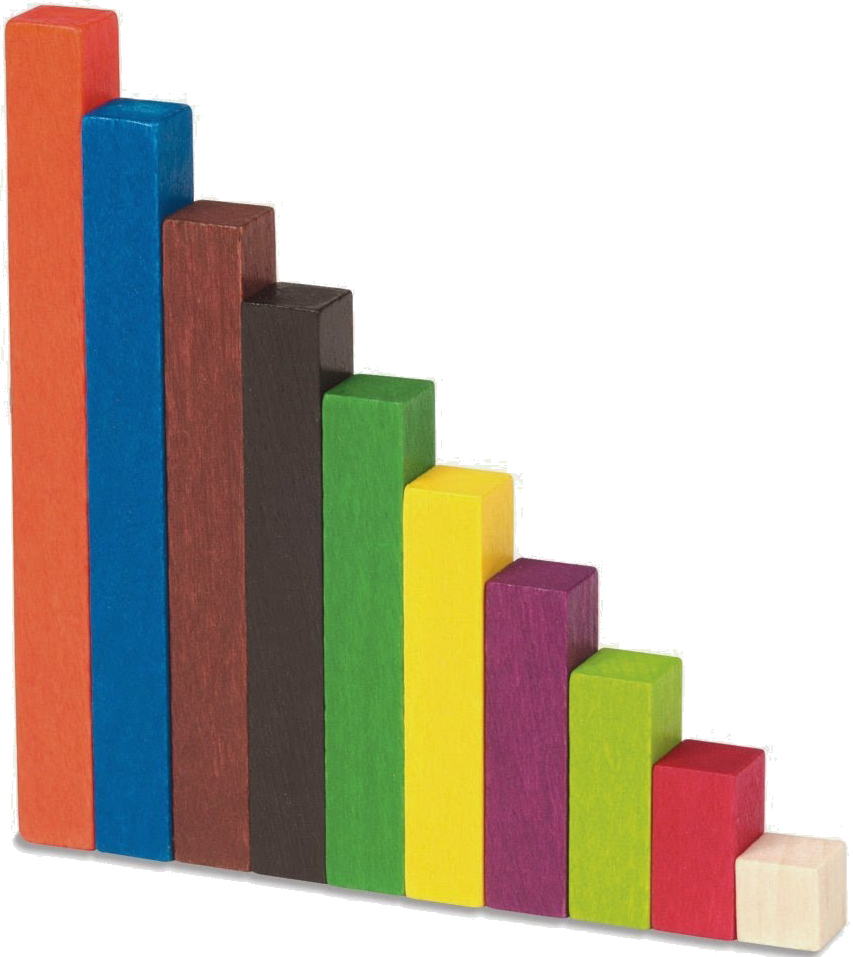
Las regletas plantean, básicamente, dos problemas de “fondo”:

Las regletas se basan en medidas de longitud, no en conjuntos de elementos con su numerosidad. Los números son anteriores a las medidas. Una longitud no se puede contar. Para que sí se pueda hacer, previamente se establece un trozo de esa magnitud como unidad de referencia, y a ese trozo se le asigna un número natural, con el que ya se puede operar: iterar, detraer, comparar, etc. Según esto, primero se debe trabajar el número y el sentido numérico, y luego sus diferentes aplicaciones.

Al basarse las regletas en medidas de longitud,  tan sólo es a través de ella como se pueden ver los incrementos o decrementos numéricos. Pero, ¿por qué no puede crecer o decrecer igualmente el grosor o la altura, ya que se trata de algo con volumen? ¿Se puede sostener el modelo de crecimiento o decrecimiento de las regletas como el adecuado para cualquier pareja de conjuntos que difieran entre sí un número determinado de elementos? Naturalmente que no.

También me parece un error grave identificar un número con un color. Precisamente el número de un conjunto es algo invariante, que no se ve influido por ninguna apariencia externa de las que se revistan sus elementos: color, grosor, materia, forma, etc. Nuestros alumnos de Infantil, desde los tres hasta los cinco años, se han iniciado en el sentido numérico y han conseguido una buena conceptualización numérica sin ese tipo de identificaciones.

Además de estas consideraciones de base, podemos añadir otras respecto a las equivalencias que se establecen con la regletas y la manipulación real que de las mismas realiza el niño.

Una de ellas hace referencia a la forma de contar los objetos que no depende de la forma, tamaño o color del objeto en sí, de manera que si podemos contar cualquier objeto de forma individual, ¿cómo explicamos al alumno que las regletas de distintas longitudes que representan dos, tres, cuatro,…unidades no las contamos también como objetos independientes, de la misma forma que hacemos con la unidad de referencia? P.e., cuando tenemos tres regletas de valor “dos unidades” decimos que equivale al seis, pero también podríamos decir simplemente que hay tres regletas o, dicho de otra forma, cuando nos encontramos en los primeros estadios de la cadena numérica, si le damos a un niño tres regletas de valor “dos unidades” y le pedimos que las cuente, nos responderá que hay tres, porque son tres objetos los que ve, al no tener la posibilidad de manipularlos para descomponerlos en unidades sueltas y no conocer las equivalencias para llegar a responder que hay seis unidades. Por tanto, estamos haciendo trabajar al alumnado en un ambiente confuso.

Otra cuestión hace referencia a que se trata de un material continuo, lo que impide su descomposición y su posterior composición. Con el número seis, p.e., se pueden buscar descomposiciones o composiciones equivalentes utilizando otras regletas, pero no con esa misma regleta al no poder partirla en unidades independientes. Las regletas nos permiten la equivalencia entre elementos distintos pero no la reversibilidad al no poderlas trocear y volver a componer el seis. En este aspecto, los bloques encajables o de construcción sustituyen con ventaja a las regletas, porque además de equivalencias también tienen reversibilidad, p.e., el conjunto de bloques encajables que forman el seis se puede componer y descomponer a partir de ella misma de varias formas distintas.

Una de los principales carencias del alumnado del sistema tradicional es precisamente la falta de dominio de las descomposiciones numéricas, más allá de la habitual en U, D y C, por no ser trabajadas adecuadamente tanto en su equivalencias como en su reversibilidad.

Si pasamos a la comparación de conjuntos con cardinales distintos, nos volvemos a topar con el mismo problema de equivalencias que dificulta su comprensión. P.e., comparando el seis y el nueve sólo podemos determinar la diferencia en más o en menos mediante el uso de la equivalencia con otras regletas, pero no podemos descomponer esa regleta como nueve unidades –reversibilidad- con las que poder establecer tres de ellas como la diferencia en más o menos. Esta función la realiza con excelentes resultados, y comprensión para el alumnado, los bloques encajables o mediante la comparación de ristras de tapones .

Esta falta de reversibilidad se extiende al cálculo de la suma y de la resta en sus diversos formatos tanto manipulativos como escritos mediante el algoritmo ABN, en el cual se muestra mucho más efectivo en sus primeros estadios el uso de palillos o cualquier otro material que se descomponga fácilmente de forma que lo que manipulativamente se hace, pase a su representación simbólica por escrito.

Podemos resumir que siendo la regletas un material muy adecuado para trabajar dentro del algoritmo tradicional, no es aconsejable su uso en el método ABN. Pero no porque no se pueda trabajar por parte del profesorado consciente de las limitaciones de este material, si no porque existen otro materiales, como los mencionados en el artículo, que cumplen mejor estas funciones y permiten la comprensión de una forma más natural e intuitiva.

Finalmente, insistimos en no imponer ni prohibir nada a nadie. Por otro lado, ¿cómo lo íbamos a hacer? Nuestras armas son exponer los argumentos que hay detrás de nuestras decisiones, confiando en su poder de convicción. Luego cada uno o una hace lo que considera necesario.