Destrezas con la división ABN
No dejo de sorprenderme con lo que son capaces de hacer algunos alumnos mediante el cálculo ABN. Lo que cuento a continuación, lo entenderán bien aquellos que conocen o trabajan el método, pero animo a todos, por curiosidad a descubrir cómo calculan algunos niños en éste método.
Se trata de Carlos, un alumno de 3º de Primaria, que empieza la división como normalmente hacen todos. En la primera fila (de derecha a izquierda), busca un número, en éste caso el 50, que al multiplicarlo por 49 (el producto lo hace mentalmente) le da 2 450, y que al restar al dividendo (4 899) le proporciona un nuevo dividendo que pone al principio de la segunda línea, el 2 449.
Y a partir de aquí está lo curioso, por que en lugar de volver a multiplicar por un número sencillo como el 10, 20, 30, 40, decide multiplicar por 49, pero nuevamente lo hace mentalmente, ¿como?.
Según la explicación que me da Carlos, en el anterior paso cómo multiplicó por 50 y le salió 2450, ahora lo único que tiene que hacer es restarle a esa cantidad 49, y por tanto el producto de 49 x 49 es 2 401.
Me resulta muy curioso el hecho de la capacidad de razonamiento que alcanzan los niños con éste método. No a todos se le ocurre una solución tan simple como la que cogió Carlos, la mayoría hubieras hecho el producto convencional, pero ahí está la chispa que distingue a los alumnos que aprenden entendiendo la operaciones, de los que méramente aplican unas reglas memorizadas para resolver las cuentas


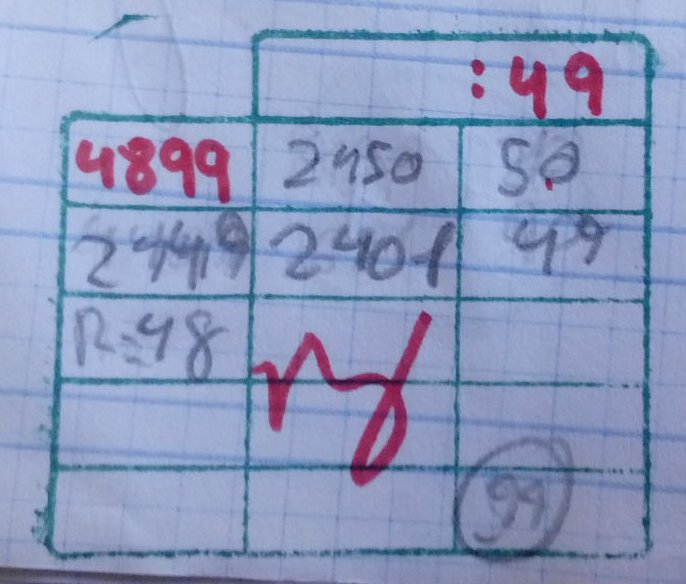



Deja una respuesta