Este es el grandioso lema que usa «Rubio blog» para anunciar los «nuevos» iCuadernos.

Pues eso, Los tradicionales Cuadernos Rubio de papel ahora en tu tablet, esos que me hicieron disfrutar tanto de pequeño y que durante algunos años hice que mis alumnos disfrutaran igualmente.

Esperemos que este salto no suponga exclusivamente eso,  pasar del papel al tablet, las abuuuuuurridas cuentas Rubio para seguir «iIguales». Como si un tablet cambiara tanto los contenidos como usar la pizarra digital a modo de una carísima tiza que evita mancharte las manos. Por si estoy equivocado os dejo, al final del artículo, el vídeo de promoción, a ver si adivináis algo.

Pero claro hablar así es muy gratuito, cualquiera puede hacerlo, pero como no se trata de criticar por criticar, ni de dar publicidad gratuita, si no de dar unas ideas  a la empresa Rubio, ya que una inversión tal requiere poder aportar algo nuevo, efectivo y si además divierte a los alumnos, como ellos indican, pues perfecto.

En primer lugar esperamos que en sus iCuadernos, por fin, desde su creación en 1956 hayan cambiado algo más de su portada. Es decir hayan incluido lo que desde ese tiempo han aportado los nuevos conocimientos sobre cómo calculan los niños; incluyan, tipifiquen y gradúen correctamente las distintas tipologías de problemas aritméticos existentes así como el  momento de su introducción, vaya a ocurrir lo de siempre: que la única razón de su éxito esté en que son los cuadernos de “toda la vida” y la falsa creencia que con ellos los alumnos aprenden.

Lo evidente es que con su uso y por extensión mediante el cálculo tradicional (o viceversa) se consta fácilmente en nuestra sociedad que ejercitar este tipo de ejercicios no ha mejorado el cálculo de la gente, las cuentas son odiadas por el alumnado, que no recibe con agrado su realización, por ser repetitivos y faltas de motivación, tampoco mejora el cálculo mental (o cálculo pensado), ya que para tal fin es necesario usar otro tipo de metodologías (Aloha, Quinzet, kumon…) unas gratuitas y otras no,  y con el remate, de usar operaciones con números muy elevados, lo cual está demostrado que no aportan nada nuevo y sin embargo inducen al error, al desánimo y al fracaso.

ALGUNAS DEFICIENCIAS EN EL CÁLCULO QUE SE LES ACONSEJA MEJORAR

– No ignoren trabajar los complementos del 10, base de nuestro sistema decimal, con los cuales los alumnos comprenderán y construirán el resto de números y operaciones.

– Trabajen la combinación de números para comprender las relaciones existentes entre ellos. Sumar todos los número con el 9, con el 8,… sumar dos veces el mismo número 5 + 5, 7 + 7.

– No caigan en la tentación de sus viejos cuaderno de pasar en muy pocas operaciones al cálculo de 2 sumandos de 2 cifras y 3 cifras, sin que estás últimas tengan un sentido concreto.

– Al proponer las cuentas tengan en cuenta la graduación de dificultad, esta no consiste en pasar de números de una, a dos, tres o cuatro cifras. Dentro de cada una existen una graduación de dificultad que permite que el alumno progresivamente conozca los entresijos de las operaciones y las dominen fácilmente.  Por ejemplo en sumas de tres sumandos de un dígito, ¿qué cuesta hacerlo bien?, ya que estamos se hace o si no lo se hace nada:

1.- Sin rebasar decenas 3 + 4 + 1
2.- Rebasando decena en la última combinación 3 + 4 + 6
3.- Rebasando decena en la primero combinación pero no en la última 3 + 8 + 6
4.- Rebasando decena en las dos combinaciones 5 + 8 + 9

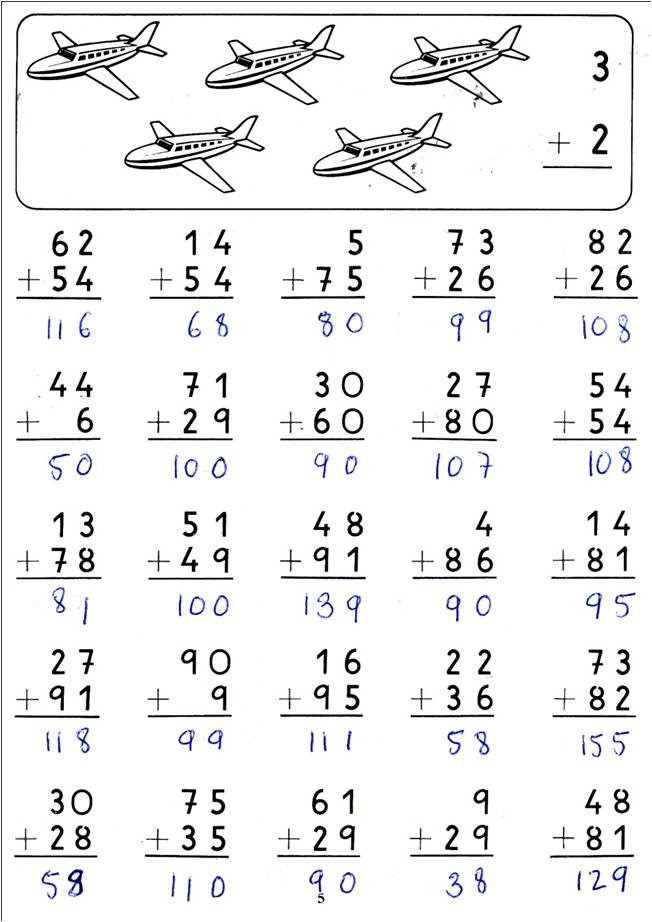
Otro ejemplo ilustrado con la página del cuaderno 1A de Rubio, para que no parezca un simple potaje de cuentas sin sentido:

Como se puede ver no se tiene en cuenta graduación alguna, mezcla unas con otras, sin que exista un hilo conductor que permite comprobar que existe una graduación pensanda como por ejemplo sería poner:

1.- Decenas completas más dígitos 20 + 8
2.- Decenas completas 20 + 30
3.- Decenas completas más decenas incompletas: 30 + 25
4.- Decenas incompletas y dígito: 38 + 5
5.- Decenas incompletas más decenas incompletas: 24 + 18 y 36 + 28
6.- Centenas completas más decenas completas más unidades, o centenas completas más decenas incompletas,…

300 + 40 + 9
300 + 49
357 + 6
428 + 9
357 + 60
357 + 63
498 + 269

Y PARA LOS PROBLEMAS… MÁS CONSEJOS

Aunque hay que aplaudirles que son los que trabajan una mayor tipología de problemas, aunque no en su totalidad, lo más mejorable es que no lo hacen en un orden lógico, ni en los cursos adecuados, dándose bastantes casos de planteamiento de problemas no adecuados al nivel al que van dirigidos (ver artículos sobre graduación de problemas matemáticos).

Pero ya que nos ponemos porqué no lo hacemos bien del todo e incluimos:

– Por qué no incluir actividades para iniciarse en la resolución de problemas.
– Incluimos una graduación que permita trabajar problemas desde imágenes que paulativamente nos lleven hasta los problemas de toda la vida, pero que durante el proceso sea posible que el alumno aprenda una sistematización para atajar los problemas.
– Incluir ejercicios de problemas para trabajar oralmente.
–  Que los primeros problemas sean breves, cocisos, con el planteamiento en líneas distintas y la pregunta en párrafo aparte. Que permita realizar estimaciones y dejar espacios para dibujar del problema.
– Y ya puestos por qué no incluimos problemas sin solución, absurdos, con falsas relaciones, para que puedan diferenciar lo que es un problema matemático de lo que no lo es.
– Y qué trabajo cuesta intentar que sean verdaderamente divertidos, entretenidos, o simplemente reales, que trabajen situaciones de la vida ordinaria, y no de camiones llenos de cajas de tomates, que por la edad de nuestros alumnos, aún queda muy lejos.

Ahí dejo unos consejos para mejor, salvo que de lo que se trate sea simplemente de mantenerlo entretenidos y que no den mucho la bara ni en clase ni en casa.