División ABN por 2 cifras con escala(sin restos parciales)
Sobre el procedimiento para la realización del Algoritmos ABN de la división ya hemos publicado varios artículos sobre el tema, «Precisiones sobre el Algoritmo ABN de la división«, «División ABN por 1 cifra» y «División ABN por 2 cifras con restos parciales«.
En este artículo se mostrará un paso más que realizan los alumnos, cuando tienen un dominio suficiente del cálculo mental, y que de forma natural logran con el objetivo de simplificar pasos.
En el artículo «División ABN por 2 cifras con restos parciales» se mostraba cómo se realiza la división descomponiendo el número y produciendo, durante el proceso, los llamados «restos parciales» que vamos incorporando a la cantidad que aún no se ha dividido.
En esta ocasión, el alumno, que ya tiene un dominio de las operaciones de multiplicación, suma, restas y del cálculo mental suficiente, lo refleja simplificando el proceso y el número de columnas necesarias.
Durante este proceso lo que debe trabajar, y el docente incidir, es en el cálculo por aproximación de la cantidad que podrá dividir, para lo cual puede ayudarse de una tabla, que llamaremos escala y que servirá de apoyo en esta labor.
Para verlo mejor mostramos dos ejemplos explicando el proceso. En el primero dividiremos 3571 entre 37
ESCALA
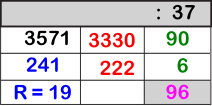
EXPLICACIÓN DE LAS COLUMNAS:
– La columna verde son las cantidades que vamos repartiendo, y cuya suma total será el resultado final en rosa. Esta cantidad es elegida por el propio alumno, de entre las que observa con más posibilidades para repartir.
– La columna en rojo indica las cantidades que ya se ha repartido, y que resulta de ir multiplicando las cantidades que ponemos en la columna verde y el divisor. Una vez finalizada la operación, la suma del total de esta columna junto con el resto nos sirve de comprobación que la división es correcta (en este caso 3330 + 222 + 19 = 3571)
-La columna azul representa las cantidades que aún no se han dividido, es decir la diferencia entre los sucesivos dividendos y la columna roja. Por ejemplo en la segunda fila el número 241 se obtiene de restar al dividendo 3571 la cantidad ya repartidas 3330.
– La escala la realizan aquel alumnado que necesita un apoyo visual de las multiplicaciones del divisor que puedan hacerle falta durante el proceso. Su elaboración es muy simple, basta con multiplicar el dividendo por la unidad seguida de ceros y por aquellas otras cifras más comunes: mitad, doble (seguidas de ceros si lo ve oportuno).
Esta escala no es obligatoria, sólo es una guía y puede realizarse en cualquier momento.
EMPEZAMOS
– La primera cifra que ponemos en el cociente dependerá de lo que el alumno vea más fácil. Si nos fijamos en la escala, dicha cifra será menor de 100, pero estará muy próxima a éste ya que como nos muestra la escala al multiplicar 37 por 100, el dividendo es sólo un poco menor. Por ello el cociente estará entre 80 ó 90.
– Ponemos en la columna de la derecha su producto: 3330
– Ponemos en la primera columna 241 la diferencia de 3571 y 3330.
– Las dos primeras cifras de nuevo dividendo nos indica que el siguiente cociente puede ser 6 ó 7, aunque este último si efectuamos la multiplicación comprobamos que nos pasamos. Por ello multiplicamos por 6 y se nos genera un reparto de 222
– Al restar al dividendo 241 el nuevo reparto de 222, nos genera un resto de 19 que al ser inferior al divisor, acaba la operación.
– Por tanto el resultado es la suma de la columna verde, 90 + 6 = 96 y de resto 19
OTRO EJEMPLO PARA DIVIDIR 8324:52
Este mismo ejemplo puedes verlo desarrollado por un alumno en el vídeo del final
– En primer lugar crea una escala del divisor multiplicado por la unidad seguida de ceros y por la mitad de la primera. Puede poner más, si los necesita, pero con estos tiene suficiente para poder realizar una estimación adecuada.
– Según esa escala al multiplicar por 100 que se aproxima bastante al dividendo, multiplica (5200) y resta al dividendo y coloca la diferencia del mismo (3124).
– En la segunda fila, multiplica por 50 que se aproxima bastante al nuevo dividendo, multiplica (2600) y resta al dividendo y coloca la diferencia del mismo (524).
– El último paso es muy fácil ya que basta multiplicar por 10 y restar al nuevo dividendo, quedando como resto 4.
– El cociente es la suma de la última columna, en verde, 160.
CONCLUSIÓN
Puede parecernos, a los que hemos aprendido con el cálculo tradicional, que este tipo de división es más compleja que la que nosotros conocemos, pero caemos en un error de posición, en el sentido de creer que el alumnado al que va dirigida la enseñanza de la operación ya conoce el proceso tradicional y por tanto le resulta más sencillo.
Sin embargo el error está en creernos nosotros, por el simple hecho de dominar el proceso, que el alumno no sólo lo hace igualmente, sino que además lo entiende.
Si somos capaces de desprendernos del proceso tradicional, veremos que este procedimiento es mucho más fácil de entender que el tradicional y por tanto al alumno le resultará más fácil, por el simple hecho de saber lo que está haciendo en cada momento con los números.
Por último un consejo, ya sabes cómo dividir con el método ABN, ahora practica un poco y te sorprenderás de lo simple que puede llegar a ser una división.


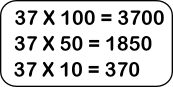

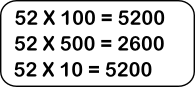



Deja una respuesta