Con este artículo acabamos la serie dedicada a la adquisión de las destrezas de contar.

2.3. Secuencias de ejercicios para la adquisición de los niveles 4 y 5 de la cadena numérica.

2.3.1. Contar de dos en dos.

2.3.2. Nivel cuatro. Contando hacia adelante.

2.3.3. Nivel cinco. Contando hacia atrás.

(NOTA: Durante los próximos días iremos completando con fichas de trabajo las actividades propuestas en este artículo)

Contar hacia detrás o hacia atrás es más difícil que hacerlo en sentido creciente. Por ello, es fácil que muchos niños se encuentren con dificultades en el desempeño de esta tarea. Es posible marcar transiciones que permitan disminuir las dificultades de esta tarea. Una secuencia de ejercicios es la que sigue, que incluye la secuencia del nivel 3 explicada en su correspondiente apartado, es la que siguiente:

SIMPLE LECTURA. Se trata de entrenar al niño en la lectura de los números en orden inverso al que habitualmente los enuncia. Una sencilla tira como la que se mostró en la recta numérica puede ser un material suficiente. El ejercicio persigue la intención de habituar al niño al nuevo orden en la enumeración de los números, a la nueva forma de aparecer los sonidos, etc. Para una mayor efectividad, este ejercicio lo podemos subdividir en dos. En el primer caso, el niño lee directamente de la tira, teniendo ésta totalmente descubierta. En el segundo caso, el niño tapa la tira, dejando al descubierto sólo el número que va a leer. Se puede pasar a la fase siguiente cuando se observe gran seguridad en la lectura que hace el niño y, sobre todo, cuando se observa que este, para leer algunos números, puede prescindir de la lectura de la tira (no se fija en ella, mira para otro lado, etc.)

ADIVINACIÓN Y COMPROBACIÓN. El cambio fundamental, respecto a la fase anterior, es que el niño no debe tener a la vista el número que tiene que pronunciar. El procedimiento a seguir es el siguiente:

• El niño tiene en su poder la tira. Deja al descubierto el primer número. Lo lee.

• A continuación, debe intentar adivinar qué número viene, y debe arriesgarse a pronunciarlo.

• Tras enunciar el número, descubre en la tira el número siguiente, y corrobora su acierto o constata su fallo.

• Vuelve a repetirse el proceso: adivinación del número, verificación, etc.

Cuando el alumno resuelva el ejercicio con seguridad y sin fallos, se pasa a la tercera y última fase.

ENUMERACIÓN. Es, sencillamente, cuando el alumno es capaz de recitar, en orden decreciente, la tira numérica sin ningún tipo de ayudas.

RETROCUENTA DE FORMA SALTEADA. Para contar hacia atrás de forma salteada, se debe seguir el camino señalado en el apartado 2.3.1.: Recitado con diferente intensidad de voz y los números alternos se piensan, pero no se dicen.

Si el retraso del niño impidiera obtener resultados, se debe intentar llevar a cabo los mismos ejercicios pero con un abanico de números mucho menor (por ejemplo, hasta el 5). Este tipo de actividades no supone ningún tipo de adorno ocioso. Saber contar hacia atrás potencia la capacidad de contar hacia adelante.

2.3.4. Subiendo y bajando por la cadena numérica.

Los ejercicios que contemplan a la vez el recorrido ascendente y descendente por la cadena numérica cumplen una evidente virtualidad: permiten establecer si el alumno reconoce un mismo territorio o espacio que es abordado desde perspectivas distintas.

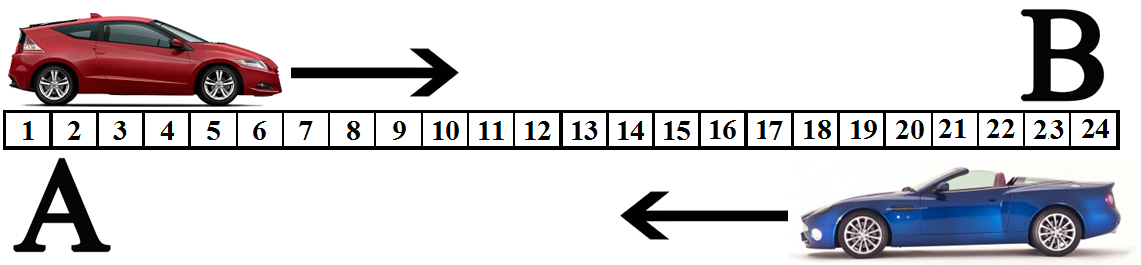
Los ejercicios toman forma (como señalamos anteriormente) de trenes que suben y bajan, que transcurren circulando con sentido opuesto: si uno va de “A” a “B”, el otro va de “B” a “A”. Además de los trenes, se admiten los modelos de escaleras o ascensores, o carreteras en que los accidentes o localidades se representan por números.

La secuencia que se propone es la que sigue a continuación:

RECONOCIMIENTO DE SI SE PRODUCE O NO LA INTERSECCIÓN. Es el caso más sencillo. El alumno se debe apercibir del punto en que se produce el cruce o intersección de los trenes o móviles que marchan en sentido distinto. Un ejercicio tipo es el siguiente:

“El coche “a” sale de su parada en dirección al “B”, y recorre 8 estaciones. El coche “b” sale de su parada en dirección al “A”, y recorre 6 estaciones. ¿Se llegan a cruzar?” (De “A” parten los trayectos ascendentes. Su primera parada es el 1, luego viene el 2, etc. De la parada “B” parten los trayectos descendentes. Su primera parada -en este caso- es el 24, le sigue el 23, etc.).

En los primeros intentos, el alumno puede efectuar realmente los recorridos, y constatar de manera efectiva si se produce o no el cruce. Pero pronto se ha de pasar a que el alumno emita el pronóstico y verifique luego si ha acertado o no.

La seguridad en la resolución de este tipo de ejercicios será el indicador que permita pasar al siguiente tipo de la secuencia.

IDENTIFICACIÓN DEL PUNTO DE INTERSECCIÓN. Este ejercicio, con respecto al anterior, sube un grado la dificultad, puesto que se trata de identificar el punto exacto de cruce o intersección. Siguiendo con el modelo del ejercicio anterior, el ejercicio que se propone a los alumnos es el que sigue:

“El “B” sale al “A”, y recorre 15 estaciones. El coche”A” sale en dirección al “B”, y recorre 14 estaciones. ¿Entre qué parada se cruzan?”

Para resolver este ejercicio hay que establecer una sencilla mecánica de resolución: dando independencia al orden en que se efectúen los movimientos, a cada adelanto de una parada de uno de los coches debe seguir inevitablemente el adelanto de una parada en el otro vehículo. Así:

• El coche A → B se sitúa en la parada 1. A continuación el coche B→A se sitúa en la parada 24.

• El coche A→B se sitúa en la parada 2. A continuación el coche B→A se sitúa en la parada 23.

• Etc.

El punto de corte o intersección se producirá entre las paradas 12 y 13.

Como en casos anteriores, la dinámica de resolución del ejercicio tiene que ir desde la realización práctica y manipulativa del mismo, hasta hallar la solución sin necesidad de efectuar los recorridos. Conseguido esto, se pasa al escalón siguiente de la secuencia.

DETERMINACIÓN DE RECORRIDOS COMUNES. Si dos coches se cruzan, necesariamente tienen que tener un territorio común que es recorrido por ambos. En el ejemplo que nos ocupa, hablaremos de paradas comunes. Un modelo de ejercicio a proponer sería el que sigue:

“El coche “B” sale de la parada en dirección al “A”, y recorre 18 estaciones. El coche “A” sale de la parada en dirección al “B”, y recorre 15 estaciones. ¿Por qué paradas han pasado los dos coches?”

Ambos coches tendrán como trayecto común las paradas que van de la 6 a la 15, ambas inclusive.

Como en casos anteriores, la dinámica de resolución del ejercicio tiene que ir desde la realización práctica y manipulativa del mismo hasta hallar la solución sin necesidad de efectuar los recorridos.

INDICE DE ARTÍCULOS PUBLICADOS

1. – Introducción

2.- Las fases de la progresión en la cadena numérica.

2.1.- La cadena numérica

2.2.- Secuenciación para la adquisición de los primeros niveles de la cadena numérica.

2.2.1.- Avisos sobre las actuales prácticas.

2.2.2.- La disposición de los objetos a contar.

2.2.3.- Ejercicios y actividades para el dominio de los niveles dos y tres de la cadena numérica.

2.3-. Secuencias de ejercicios para la adquisición de los niveles cuatro y cinco de la cadena numérica.

2.3.1.- Contar de dos en dos.

2.3.2.- Nivel cuatro. Contando hacia adelante.

2.3.3.- Nivel cinco. Contando hacia atrás.