La prueba del 9
 En mayo de 2009 el ovíparo publicó en su blog «Todos no somos mamíferos» (Que recomiento al colectivo educativo, por su originalidad y frescura de artículos) un par de artículos dedicados a la prueba del 9, tanto para la multiplicación como para la división.
En mayo de 2009 el ovíparo publicó en su blog «Todos no somos mamíferos» (Que recomiento al colectivo educativo, por su originalidad y frescura de artículos) un par de artículos dedicados a la prueba del 9, tanto para la multiplicación como para la división.
Ambos artículos me recordarón los tiempos en los que esa prueba era habitual para comprobar el resultado de esas largas operaciones matemáticas. Hoy en día estas pruebas han desaparecido hasta de los libros de texto. Sin embargo un comentario dejado en su blog sobre la prueba, me recordó que un profesor de bachillerato, hablando sobre el tema, nos enseño la prueba del 11 ya que la del 9 no era infalible en todos los casos y que se podían producir «falsos positivos» en los cuales la prueba decía ser correcta una operación que no lo era.
PRUEBA DEL NUEVE
Para realizar la prueba del nueve tenemos que:
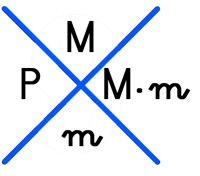
– Dibujamos una aspa o cruz.
– Sumamos los distintos números que forman cada cifra (la del multiplicando, multiplicador, producto, dividendo, divisor,…) y dividimos el total por 9 o vamos restando 9 cada vez que se supere esta cifra.
– Al final en cada cifra tendremos un resto menor a 9
– Ese resto lo colocaremos en la zona de la cruz que corresponda a cada cifra.
– La operación estará bien si las dos cifras de la zona horizontal de la cruz coinciden.
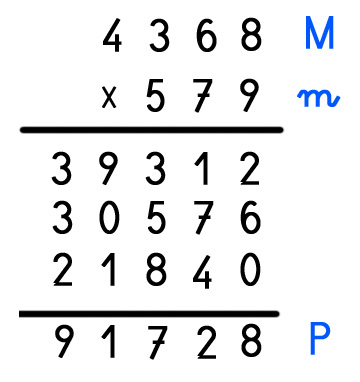
EJEMPLO EN EL PRODUCTO:
M = Multiplicando (En el ejemplo 4368)
m = Multiplicador (En el ejemplo 579)
P = Producto (En el ejemplo 2529072)
Ejemplo de multiplicación que cumple la prueba del 9:
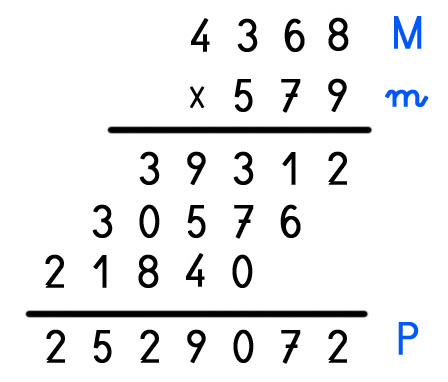 4 + 3 + 6 + 8 = 21 : 9 = 2 RESTO 3
4 + 3 + 6 + 8 = 21 : 9 = 2 RESTO 3
5 + 7 + 9 = 21 : 9 = 2 RESTO 3
2+5+2+9+0+7+2= 27 : 9 = 3 RESTO 0
Sin embargo veamos que la prueba también da correcta si nos equivocamos a la hora de colocar las cifras de los productos intermedios antes de sumarlas.
4 + 3 + 6 + 8 = 21 : 9 = 2 RESTO 3
5 + 7 + 9 = 21 : 9 = 2 RESTO 3
9+1+7+2+8= 27 : 9 = 3 RESTO 0
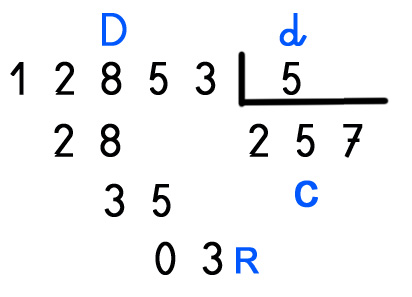
EJEMPLO EN LA DIVISIÓN:
Los términos son:
D = Dividendo (En el ejemplo )
d = divisor (En el ejemplo )
c = cociente (En el ejemplo )
Ejemplo de división que cumple la prueba del 9:
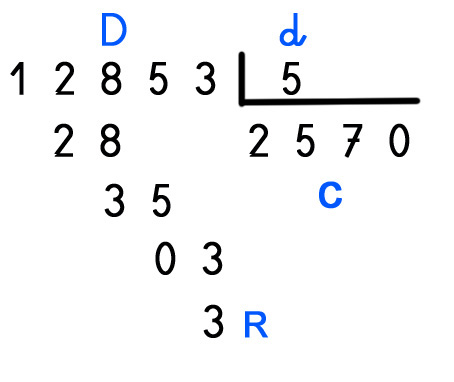
1 + 2 + 8 + 5 + 3 = 19 : 9 = 2 RESTO 1
5 = 5 : 9 = 0 RESTO 5
2 + 5 + 7+ 0= 14 : 9 = 1 RESTO 5
Sin embargo, y al igual que en la multiplicación, supongamos que nuestros alumnos/as cometen el error de no dividir la última cifra y no ponen el cero en el cociente.
1 + 2 + 8 + 5 + 3 = 19 : 9 = 2 RESTO 1
5 = 5 : 9 = 0 RESTO 5
2 + 5 + 7 = 14 : 9 = 1 RESTO 5
Como vemos la denominada prueba del 9 no es infalible, y aunque sin embargo es muy útil cuando tenemos que comprobar multiplicaciones o divisiones largas, en las que no tenemos calculadora o absurdamente no nos la permiten, es un método bastante fiable para saber si nos hemos equivocado o no.
En el siguiente artículo explicamos la prueba del 11, en la que no se da este pequeño problema.


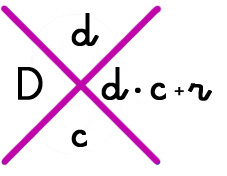
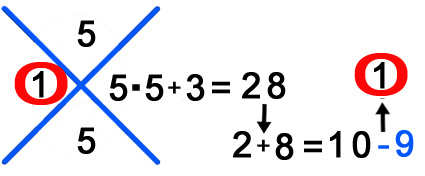



Deja una respuesta