La prueba del 11
 Cómo comenté en al prueba del 9, vamos a ver otro prueba cuyos resultados son más fiables que la anterior. Para ello vamos a utilizar las mismas operaciones que hemos usado en la demostración con la prueba del 9 y que nos han dado faltos positivos tanto en la multiplicación como en la división.
Cómo comenté en al prueba del 9, vamos a ver otro prueba cuyos resultados son más fiables que la anterior. Para ello vamos a utilizar las mismas operaciones que hemos usado en la demostración con la prueba del 9 y que nos han dado faltos positivos tanto en la multiplicación como en la división.
Se trata de una prueba similar a la anterior aunque con una pequeña variante, nada complicada. Pero antes veamos los pasos para aplicar la prueba del 11:
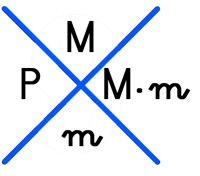
1.- Al igual que en la prueba del 9 dibujamos una aspa o cruz. (En el ejemplo las letras indican dónde debemos escribir las cifras correspondiente a cada número)
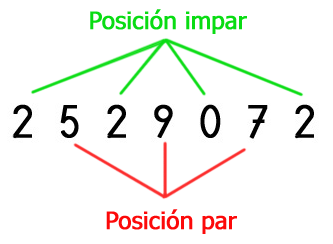
2.-Sumamos las cifras pares e impares por separado de cada (la del multiplicando, multiplicador, producto, dividendo, divisor,…). El par o impar se refiere a la posición que ocupa la cifra en el número, no a si dicho número es par o impar. Veamos un ejemplo:
En este ejemplo sumamos juntos los que están en cada posición:
Posición impar: 2 + 0 + 2 + 2 = 6
Posición par: 7 + 9 + 5 = 21.
2.- En cada número, una vez que tengamos la suma de impares por un lado y pares por otro, realiza la diferencia de la suma de los impares menos la de los pares. Pero ten en cuenta que si la suma de los impares es menor que la de los pares le vamos a sumar 11 a los impares. tantas veces hasta que supere a los pares (También puedes restarle 11 a los impares pero para los niños/as en más lioso porque aveces tenemos que sumar también en los impares). En nuestro ejemplo:
Cómo la suma de los impares es 6 (menor que los pares 21) sumamos 22 (11 + 11) para que supere la suma de par que es 21, quedando la siguiente resta:
28 – 21 = 7
3. – A continuación dividimos el resultado de la resta entre 11 y el resto será lo que pongamos en donde corresponda en la cruz o aspa que hemos dibujado. En nuestro ejemplo pondríamos el 7
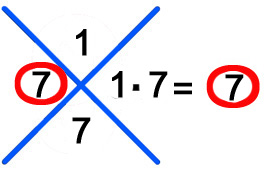
4.- La operación estará bien si las dos cifras de la zona horizontal de la cruz coinciden.
EJEMPLO EN EL PRODUCTO:
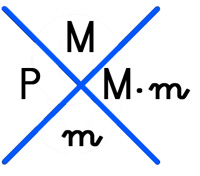
M = Multiplicando (En el ejemplo 4368)
m = Multiplicador (En el ejemplo 579)
P = Producto (En el ejemplo 2529072)
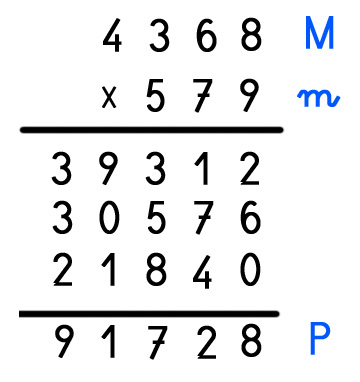
Ejemplo de multiplicación que cumple la prueba del 11:
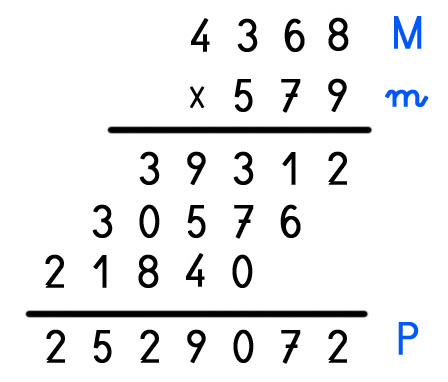 Impares (8 + 3 = 11) Pares (4 + 6 = 10); 11 – 10 = 1 RESTO 1
Impares (8 + 3 = 11) Pares (4 + 6 = 10); 11 – 10 = 1 RESTO 1
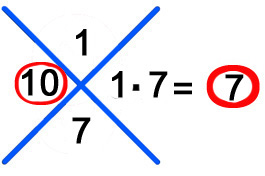
Impares (9 + 5 = 14) Pares (7); 14 – 7 = 7 RESTO 7
Impares (2 + 2 + 0 + 2 = 6) Pares (5 + 9 + 7 = 21); 28 – 21 = RESTO 7
Veamos qué ocurre si la operación está mal hecha (En la prueba del 9 nos daba un falso positivo).
Impares (8 + 3 = 11) Pares (4 + 6 = 10); 11 – 10 = 1 RESTO 1
Impares (9 + 5 = 14) Pares (7); 14 – 7 = 7 RESTO 7
Impares (9 + 7 + 8= 24) Pares (1 + 2 = 3); 24 – 3 = 21 : 11 RESTO 10
En este caso no coinciden indicándonos que la operación está mal.
EJEMPLO EN LA DIVISIÓN:
Los términos son:
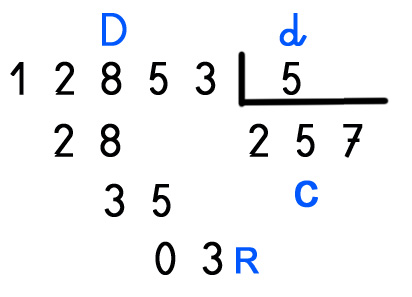
D = Dividendo (12853)
d = divisor (5 )
c = cociente (2570 )
Ejemplo de división que cumple la prueba del 11:
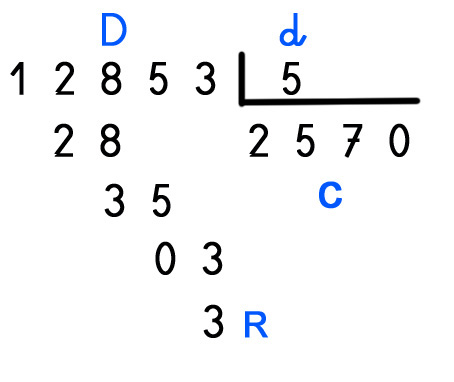
Impares (1 + 8 + 3 = 12) Pares (5 + 2 = 7); 12 – 7 = 5 RESTO 5
Impares (5) Pares (0); 5 – 0 = 5 RESTO 5
Impares (5 + 0 = 5) Pares (2 + 7 = 9);
(5+11) – 9 = 7 RESTO 7
Veamos qué ocurre si la operación está mal hecha (En la prueba del 9 nos daba un falso positivo).
Impares (1 + 8 + 3 = 12) Pares (5 + 2 = 7); 12 – 7 = 5 RESTO 5
Impares (5) Pares (0); 5 – 0 = 5 RESTO 5
Impares (2+7) Pares (5); 9 – 5 = 4 RESTO 4
Como vemos la prueba del 11 tampoco ha fallado en esta ocasión, pero la pregunta que nos queda para acabar sería ¿para qué sirve hoy en día este tipo de comprobación?.
Cómo indicaba en la prueba del 9 se trata de una prueba que no tiene mucho sentido como comprobación ya que con la calculadora comprobamos rápidamente si la operación se hizo bien o no, aunque nunca está demás saber una cosa más y practicar las operaciones matemáticas simples.


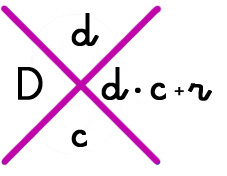
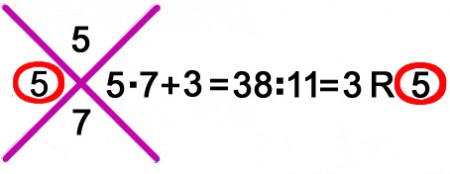
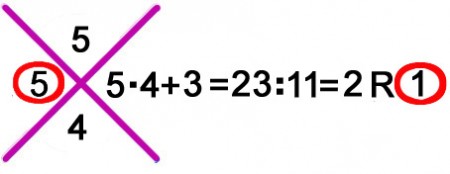



Deja una respuesta