Las formas geométricas espaciales presenta, a veces, gran dificultad de comprensión, debido a una escasa visión espacial, en gran parte consecuencia de tener que representar sobre el plano lo que se ve en el espacio. Por tanto, conviene tener muy claros los elementos fundamentales de la geometría del espacio, que son el punto, la recta y el plano.

Las siguientes figuras geométricas son ilusiones ópticas que no son posibles en la realidad y en último término consisten en la exclusión velada de algunos axiomas de la geometría euclídea.

En clase podemos trabajarlas pidiendo que los  alumnos/as describan el por qué no son posibles.

Esta primera imagen está realizada por Erik Johansson  y se basó para ello en la imagen dibujada por primera vez en 1934 por Reutersvärd y que dejamos a continuación junto con otras versiones de la misma.Puedes ampliar el tamaño haciendo clic sobre ellas.

Figuras realizadas por Escher a partir del trial realizado por Reutersvärd

Esta imagen aparece en el interesante libro de Bruno Ernst » Adventures with impossible figures» (Tarkin Publications, Norfolk, 1986) bajo la frase «las cosas no son siempre lo que parecen».

Cubo de Necker, aparentemente normal, hasta que notamos que algo «no encaja» y que no podría ocurrir si dicha figura existiera en realidad.

Jugamos con líneas paralelas en distintos planos buscando la tridimensionalidad en el plano y el resultado es un tanto paradójico.

La siguiente pirámide fue realizada por H.J. Verwaal

Estrella de David de Stanford Slutsky

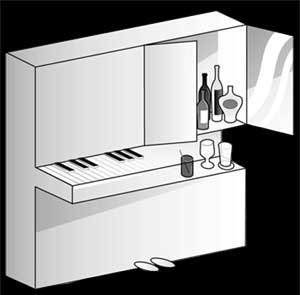
Para terminar este «Piano – mueble bar» muy particular. ¿Por qué?. Si sabeis del autor informarlo en los comentarios.

Para acabar este alfabeto creado por Laurent Lacroix basado en el efecto Escher.